Trong văn bản mới này, tôi sẽ nói về Alphanumeric Qabbala , một loại mật mã mà tôi đã khám phá (hơi chưa đầy đủ) trong phần thứ 3 của cuốn Lịch sử mật mã Thelemic , mặc dù lần này cách tiếp cận của tôi sẽ rất khác so với các bài viết trước. Lý do cho điều này là trong văn bản đầu tiên của tôi về mật mã đó, tôi đã phải tập trung một chút vào nguồn gốc của nó – xét cho cùng, tôi không viết về Lịch sử của mật mã sao? – và khi tôi làm điều đó, có rất nhiều thứ thú vị khác chưa được đề cập đến. Vì vậy, trong bài viết mới này, vì tôi không phải giải thích lại lịch sử của nó, thay vào đó, tôi sẽ tập trung vào những gì chúng ta có thể làm với mật mã này, cũng như cách chúng ta có thể khám phá một số tính chất rất kỳ lạ của nó.
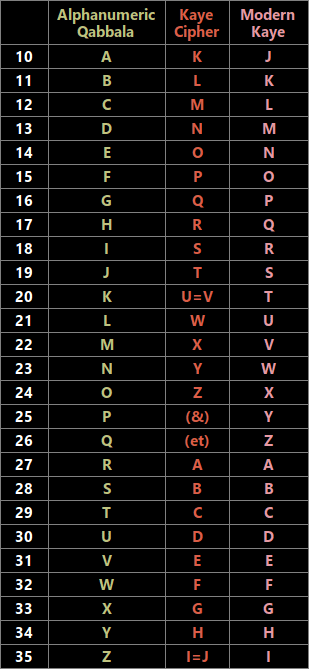
Là phần giới thiệu mới về mật mã này, tôi sẽ bắt đầu bằng cách giải thích chính xác Qabbala chữ và số là gì và cách nó được kết nối với ký hiệu Base-36.
Tiếp theo, tôi sẽ nói ngắn gọn về một số sự đồng bộ rất kỳ lạ đã xảy ra trong cuộc đời tôi khi tôi tìm thấy và sau đó được cho biết về mật mã này, vì tôi tin rằng chúng rất đáng được lưu ý và nên được đề cập trong bài viết này. Rốt cuộc, nhờ một sự đồng bộ rất kỳ lạ mà tôi đã tìm thấy mật mã này… vậy tại sao không nói về nó?
Sau đó, tôi sẽ nói về (các) tên mật mã này, các giá trị Gematria và các tính chất toán học của chúng. Trong phần này, mục đích chính của tôi là chỉ cho Độc giả của tôi cách một số tên có thể được nghĩ ra để trả về một giá trị số rất cụ thể và dự kiến, khi được “giải mã” thông qua Gematria. Trong trường hợp này, Alphanumeric Qabbala là một mật mã có tên đã được mã hóa rất nhiều trong quá khứ để chúng có thể được kết nối cụ thể với số 36 .
Sau đó, tôi sẽ nói về cách chữ và số Qabbala liên quan đến ký hiệu Cơ số 36, một số tính chất thú vị của cơ số đó và lý do tại sao tôi nghĩ rằng chuỗi chữ và số từ 0 đến Z cực kỳ linh hoạt và cần được khám phá thêm, ngay cả đối với người sáng tạo. hoặc mục đích giải trí. Trong phần này , tôi cũng sẽ giải thích cách dãy chữ và số 0-Z có thể được sử dụng để mã hóa, mã hóa hoặc thậm chí áp dụng cho Chiêm tinh học, sau một số thử nghiệm của tôi với nó.
Trong phần sau, tôi sẽ cho bạn thấy một số phát hiện của tôi với AQ trong ngữ cảnh của Thelema và lý do tại sao tôi nghĩ rằng mật mã này có thể cực kỳ phù hợp trong ngữ cảnh cụ thể đó. Một số tài liệu này đã được trình bày trong văn bản trước đây của tôi về mật mã này, trong khi một số tài liệu khác sẽ hoàn toàn mới — và cực kỳ hấp dẫn .
Trong chương thứ hai đến chương cuối cùng, tôi sẽ nói ngắn gọn về những điều “nên” và “không nên” với Qabbala Chữ và Số, từ đó phản ánh cách tôi làm việc với AQ — và một số cách khác mà tôi nghĩ chúng ta nên làm’ t làm việc với AQ.
Và cuối cùng, vì tôi muốn để lại những điều hay nhất sau cùng, nên phần cuối cùng của văn bản này sẽ đưa ra một câu đố cho Độc giả của tôi — hay tốt hơn nữa, là một loạt câu đố .
- Chữ và số Qabbala là một nhánh của ký hiệu Base-36;
- Sự đồng bộ kỳ lạ liên quan đến Thời gian, mật mã này và con số 36;
- Tên của mật mã này (“AQ”, v.v.) và cách chúng được mã hóa mạnh mẽ;
- Cấu trúc toán học và tính chất của AQ;
- Đếm ngón tay với AQ;
- Sử dụng AQ để mã hóa và sigilization;
- Áp dụng AQ vào Chiêm tinh học (kỹ thuật mới);
- Vai trò (thường bị đánh giá thấp) của AQ trong bối cảnh Thelemic;
- Một số cách tôi có xu hướng sử dụng mật mã này.
Để bắt đầu, trước tiên hãy để tôi nói về cách AQ liên quan đến ký hiệu Base-36.
Máy tính của tôi chỉ là những sửa đổi đơn giản của công việc trước đây của Virroco, trong phạm vi kiến thức lập trình (rất) hạn chế của tôi cho phép tôi làm được. Vì vậy, cảm ơn anh ấy, không phải tôi, vì những công cụ tuyệt vời này.
Chữ và số Qabbala và số Base-36

Nhưng chính xác ký hiệu Base-36 là gì? Trên thực tế, nó giống như ký hiệu thập phân, ký hiệu mà chúng ta sử dụng hàng ngày, nhưng thay vì chỉ sử dụng mười chữ số Ả Rập từ 0 đến 9, nó cũng bao gồm 26 chữ cái của Bảng chữ cái tiếng Anh hiện đại dưới dạng các chữ số. Bạn có thể tìm hiểu thêm về ký hiệu Base-36 tại đây và tại đây — đồng thời đọc lịch sử của một công ty công nghệ được đặt tên theo ký hiệu Base-36 .
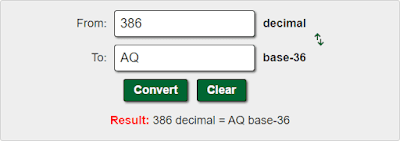
Vì vậy, làm thế nào nó hoạt động, thực sự? Trong ký hiệu thập phân (Cơ sở-10), mọi số được viết dựa trên 10 giá trị có thể (từ 0 đến 9) cho hàng đơn vị, hàng chục và hàng trăm — vì vậy, trong ký hiệu Cơ sở-36 có 36 giá trị có thể (từ 0 đến Z=35) cho đơn vị (1), “chục” (36) và “hàng trăm” (36×36). Nói cách khác, số được viết là 360 trong Base-10, nghĩa là ” 3 ×100 + 6 ×10 + 0 ×1″ , sẽ được viết là A0 trong Base-36, nghĩa là ” 10 ×36 + 0 ×1 ” .
- UnitConverters.net
- Bảng chuyển đổi số
- Đồ chuyển đổi (bản gốc)
- … hoặc bạn chỉ cần sử dụng Gematria Kabala. Nếu bạn nhấp chuột phải vào một số trong bảng chứa các mật mã đang hoạt động, bạn sẽ thấy cách số đó được viết trong các cơ số khác nhau, bao gồm Nhị phân (cơ sở-2), Bát phân (cơ sở-8), Thập lục phân (cơ sở-16) , Base-36, trong số những thứ khác.
Trong khi chờ đợi, hãy để tôi kể cho bạn nghe về…
Sự đồng bộ đầu tiên của tôi với AQ
Trong phần này, tôi sẽ cho bạn biết làm thế nào tôi biết được mật mã này: hay thực tế là làm thế nào tôi chỉ phát hiện ra rằng nó đã tồn tại sau khi tôi tự nghĩ ra nó.
Công việc của tôi với AQ bắt đầu vào những ngày cuối tháng 4 năm 2021, khi tôi lần đầu tiên được biết về mật mã này. Có rất nhiều điểm đồng bộ liên quan đến khám phá này và tôi nghĩ rằng đã đến lúc phải nói về chúng. Xin lưu ý rằng tôi đã được cấp quyền đăng ảnh chụp màn hình các phần trong cuộc hội thoại của mình. Điều này rất quan trọng để cung cấp cho phần trình bày này một số bối cảnh đồ họa và để lưu ý một số chi tiết quan trọng.
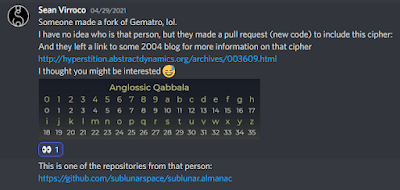
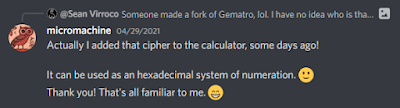

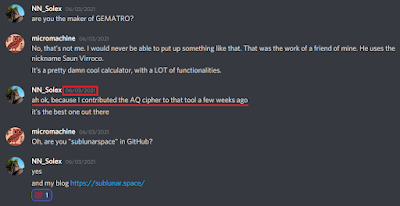
Đây là sự đồng bộ tuyệt vời đầu tiên của tôi với AQ, mặc dù nó chỉ mới bắt đầu. Kể từ lúc đó, tôi sẽ nhìn thấy con số 36 ở khắp mọi nơi và liên tục, mỗi ngày – giống như trường hợp khi tôi đang ăn tối trong khi một trận bóng đá đang được truyền trên TV. Lần thứ hai tôi nhìn vào TV, chính xác là 36 phút 36 giây đã trôi qua kể từ khi trận đấu bắt đầu. Thành thật mà nói, tất cả đều khá hoang dã.
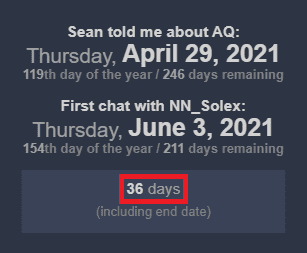
Sự đồng bộ tuyệt vời cuối cùng của tôi (tính đến thời điểm này) với mật mã này đã xảy ra vài tháng sau đó, vào cuối tháng 11 năm 2021.
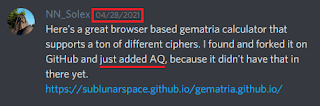
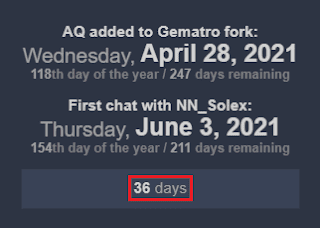
Ai mà đoán được?! chính xác là 36 ngày. ?
Tuy nhiên, một số điều “kỳ lạ” khác đã xảy ra trong ngày này. Bạn thấy đấy, tôi đã tìm thấy ngày chính xác khi AQ được thêm vào nhánh Gematro của NN_Solex vào ngày 25 tháng 11 ᵗʰ . Cộng ngày và tháng, bạn sẽ có 11+25 = 36 . Vào ngày này cũng có 36 ngày còn lại cho đến khi kết thúc năm:

Và trong trường hợp “thông điệp” không được hiểu … vào cùng ngày hôm đó, khi tôi đến nơi làm việc của mình và sau khi nhận thấy tất cả các mẫu liên quan đến số 36, tôi tò mò muốn biết số ID của công nhân là gì một đồng nghiệp của tôi – một phụ nữ xinh đẹp mà tôi “phải lòng”. Chà… bạn sẽ không tưởng tượng được tôi cảm thấy thế nào khi nhìn thấy tấm thiệp của cô ấy với số… 36 . Tôi không nói nên lời, vì những lý do rõ ràng.
Bây giờ, một hoặc hai từ về:
tên và thuộc tính của nó
Tại thời điểm này, tôi nên nói rằng đây là mật mã yêu thích tuyệt đối của tôi cho đến nay và tôi đã chơi rất nhiều với nó. Nó cũng là một trong những mật mã được đặt tên thông minh nhất mà tôi từng biết, và lý do tại sao tôi nói điều này có liên quan đến… à, tất nhiên, tên của nó!
Trong phần này, chúng ta sẽ tìm hiểu cách một số tên có thể được mã hóa bằng Gematria, sao cho chúng khớp với các giá trị được xác định trước. Chữ và số Qabbala là ví dụ hoàn hảo về mật mã có tên được mã hóa một cách tự nguyện, để chúng có liên quan cụ thể đến số 36 – vì những lý do rõ ràng.

Vì vậy, về cơ bản, tên của mật mã giải thích nó là gì:
AQ = 0123456789 + abcdefghijklmnopqrstuvwxyz

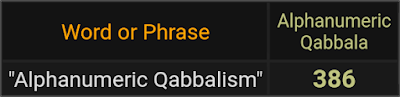
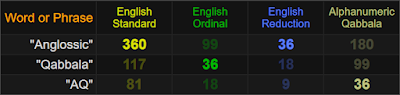
Từ văn bản trước của tôi về mật mã này , Độc giả của tôi sẽ nhớ rằng một tên gọi khác của mật mã này là Anglossic Qabbala . Ý nghĩa của thuật ngữ “Anglossic” có thể không rõ ràng đối với Độc giả của tôi, nhưng tôi sẽ chỉ nói rằng nó dường như là một từ mới có nguồn gốc từ Anglo~ (tức là có liên quan đến tiếng Anh) cộng với hạt gloss của Hy Lạp~ có liên quan đến ” lưỡi” hoặc “ngôn ngữ”… vì vậy sẽ chỉ là một cách nói hoa mỹ rằng đây là một Qabbala dành cho ngôn ngữ tiếng Anh .
Tuy nhiên, ngay cả trong trường hợp này, vẫn còn nhiều điều ngoài sức tưởng tượng. Nếu bạn tình cờ sử dụng máy tính GemCon của tôi , bạn sẽ thấy ba trong số các mật mã được bật theo mặc định là: English Standard (còn được gọi là “Extended”) , Ordinal (mật mã tiếng Anh hiện đại đơn giản nhất, từ A=1 đến Z= 26) và Phép rút gọn (còn gọi là “Số học Pythagore”) . Tôi thích sử dụng ba mật mã đó cùng nhau vì chúng hoạt động như một loại “quãng tám”, với Tiêu chuẩn là quãng tám cao hơn của Thông thường và Giảm là quãng tám thấp hơn của nó. Đối với những điều này, tôi đã thêmAlphanumeric Qabbala, bởi vì … tốt, bạn đã biết tại sao, nếu không thì bạn sẽ không đọc được điều này.
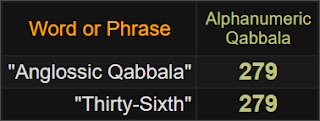
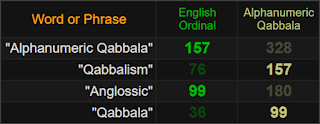
Tại thời điểm này, một số Độc giả của tôi có thể tự hỏi: “Điều này thực sự có nghĩa là gì ?” . Chà, bên cạnh thực tế là mật mã này dường như có xu hướng thu hút sự trùng hợp ngẫu nhiên, thực tế là những cái tên được đặt cho AQ này đều được mã hóa rất nhiều để tất cả chúng sẽ xoay quanh số 36 – chính xác là giá trị của cơ số từ mà AQ đã được bắt nguồn. Vì vậy, trên thực tế, điều này có nghĩa chính xác là thế này: người ta có thể sử dụng Gematria một cách sáng tạo , để mã hóa các tham chiếu bí mật trong một từ, cụm từ hoặc văn bản, sao cho những gì người ta định truyền đạt chỉ có thể được “mở khóa” (giải mã) bằng chính xác. “chìa khóa” (mật mã).
Lấy ví dụ này về một câu đố được mã hóa như vậy:
Cái tên ” A lphanumeric G ematria” gần như hoàn hảo;
Để trở nên hoàn hảo, bạn chỉ cần thêm 1 vào nó.
Tại sao?
Tôi mời bạn cố gắng giải quyết điều này. Hãy đọc thật kỹ những gì tôi đã viết cho đến thời điểm này, và câu trả lời sẽ có ở đó. Điều này thực sự có thể giúp bạn phát hiện ra những thứ được mã hóa sẵn sàng, miễn là các manh mối được đưa ra và bạn có thể hiểu chúng.
Bây giờ, bỏ qua câu hỏi về (các) tên của mật mã, chúng ta hãy chú ý đến số 36 và các thuộc tính của nó, đồng thời xem chúng ta có thể “làm gì” với nó.
Khi tôi bắt đầu thử nghiệm những thuộc tính này của mật mã AQ, ý định của tôi là cố gắng tìm ra manh mối nào đó cho một “mẫu” trong bảng chữ cái tiếng Anh. Xét cho cùng, có một số giả thuyết khác nhau về việc tiếng Anh là một “ngôn ngữ kỳ diệu” với bảng chữ cái có cấu trúc kỳ diệu:
Nhưng có một chi tiết rất hấp dẫn về điều này. Trong Những lời dạy bí mật của mọi thời đại , trong chương về Toán học Pythagore , Manly P. Hall trích dẫn Plutarch (từ “De Iside et Osiride” : đâylà văn bản trực tuyến, bao gồm cả bản gốc tiếng Hy Lạp):
“Những người theo chủ nghĩa Pythagore thực sự còn đi xa hơn thế này, và tôn vinh các số chẵn và sơ đồ hình học với tên và tước vị của các vị thần. Do đó, họ gọi tam giác đều là Minerva và Tritogenia, bởi vì nó có thể được chia đều bởi ba đường vuông góc được vẽ từ mỗi của các góc. Vì vậy, đơn vị mà họ gọi là Apollo, đối với số hai, họ đã gắn tên của xung đột và táo bạo, và đối với số ba, công lý. Bởi vì, gây thương tích là cực đoan đối với một bên, và đau khổ một bên là cực đoan ở một bên, và đau khổ ở giữa chúng. Tương tự như vậy, số 36 , Tetracys , hay Quaternion thiêng liêng của chúng, bao gồm bốn số lẻ đầu tiên được cộng với bốn số chẵn đầu tiên, như thường được báo cáo, được họ coi là lời thề trang trọng nhất mà họ có thể thực hiện, và được gọi là Kosmos.”
Đoạn này và đoạn sau giải thích một số tương ứng “thần thánh” đối với các con số theo thuyết Pythagore. Nó cũng đề cập rằng Tetraktys , hay Bộ bốn thiêng liêng , được đại diện bởi số 36, là biểu tượng quan trọng nhất của họ và được gọi là Vũ trụ. Và mặc dù dạng Tetracys được biết đến rộng rãi nhất tương ứng với số 10 (hoặc 1+2+3+4), nhưng trong trường hợp này, Plutarch lại nói rằng 36 cũng được coi là một Tetracys của Pythagore. Tôi không biết điều này trước khi tôi đọc cuốn sách của Hall.
Trong Những câu thơ vàng của Pythagoras , câu 47, sự tôn kính tương tự dành cho Tetracys:


Con số 36 dường như cũng đóng một vai trò quan trọng khi nói đến con số thiêng liêng trong thần thoại trên toàn thế giới, trong nhiều trường hợp là bội số của 36. Lấy ví dụ:
108 là một con số rất phù hợp trong Ấn Độ giáo, với những câu thần chú cụ thể được lặp lại chính xác 108 lần. Nó bằng 3×36, có nghĩa là nó được viết là 30 trong ký hiệu Base-36 (nghĩa là 3 ×36 + 0 );
Trong chủ nghĩa thần bí của người Do Thái cũng có truyền thống về Lamed Vav Tzaddikim , hay 36 Người Công Chính Ẩn Mình, theo đó “có không ít hơn 36 người công chính trên thế giới chào đón Shekhinah trong mỗi thế hệ” . Theo truyền thống này, thế giới sẽ đi đến hồi kết nếu thiếu vắng một trong số họ.
Trong Cơ đốc giáo cánh chung, con số 144 (đặc biệt là 144.000) có một vai trò cơ bản, đại diện cho các Tôi tớ của Chúa, số lượng linh hồn sẽ được cứu vào Ngày Phán xét Cuối cùng. 144 bằng 4 × 36 và nó được viết là 40 trong Base-36;
Có nhiều ví dụ khác về điều này, chẳng hạn như số giây trong một ngày, 86.400 (864 = 24 × 36), khoảng thời gian 1260 ngày được nhắc đến nhiều lần trong Sách Khải Huyền (1260 = 35 × 36) , hoặc số độ trong một vòng tròn (360 = 10 × 36).
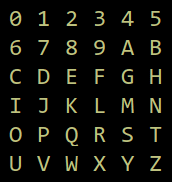
Và cuối cùng… điều này thực sự đã cho tôi một ý tưởng khác – và đó là điều tôi sẽ nói bây giờ.
Bảng chữ cái tiếng Anh và Quảng trường ma thuật của Mặt trời
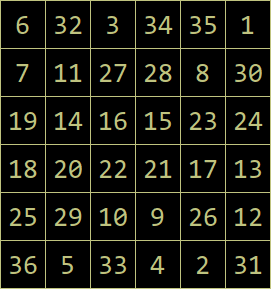

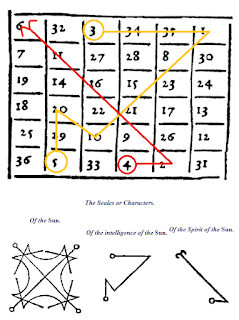
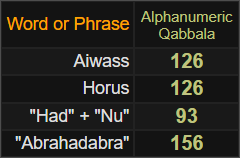
Trong “Ba cuốn sách về triết học huyền bí” của Heinrich Cornelius Agrippa , Quyển 2, chương 12 ( liên kết ), tác giả đã trình bày các dấu hiệu của trí thông minh & tinh thần hành tinh, dựa trên một kỹ thuật tạo dấu hiệu khéo léo. Sử dụng ví dụ về Mặt trời và hình vuông ma thuật 6×6 của nó, đồng thời áp dụng kỹ thuật này cho tên của trí thông minh mặt trời (Nakiel נכיאל ) và tinh linh mặt trời (Sorath סורת ), trước tiên chúng ta bắt đầu bằng cách tìm các giá trị tương ứng cho các chữ cái. Hãy phân tích “Nakiel” trước:
- Giá trị giảm của Nun là 5;
- Giá trị tiêu chuẩn của Kaph là 20;
- Giá trị chuẩn/thứ tự của Yod là 10;
- Giá trị của Aleph là 1;
- Và giá trị giảm của Lamed là 3.
- Trong trường hợp “Sorath”, được viết bằng các chữ cái Samech – Vav – Resh – Tav , chúng ta có:
- Cả Samech và Vav đều có giá trị giảm là 6;
- Giá trị giảm của Resh là 2;
- Và cuối cùng, giá trị giảm của Tav là 4.

Bên cạnh điều này, mà tôi tin rằng không hơn gì một sự trùng hợp ngẫu nhiên, trong những thí nghiệm ban đầu của tôi với kỹ thuật này, chỉ có một trường hợp khác thu hút sự chú ý của tôi. Bìa ấn bản của Simon về cuốn sách hư cấu huyền thoại (và thường bị hiểu lầm có tên là) Necronomicon chứa một dấu hiệu, bằng cách nào đó, giống một cách kỳ lạ với dấu hiệu chữ và số của “Necronomicon”
Ngoài điều này ra, thực sự không có nhiều điều để nói về kỹ thuật sigilization này, ngoại trừ việc bạn có thể sử dụng nó theo mọi cách bạn muốn. Để tìm các mẫu, để thiết kế các mẫu, như một chữ ký cá nhân, như một biểu tượng ma thuật – giới hạn thực sự là trí tưởng tượng của chính bạn.
Trong phần tiếp theo, nhưng vẫn giữ hình vuông ma thuật chữ và số này trong tâm trí của chúng tôi, hãy nói về:
Mật mã & Qabbalism chữ và số


Mặc dù mật mã ADFGVX được sử dụng theo một mẫu mã hóa nhất định (sử dụng từ khóa, sắp xếp lại thứ tự các cột, v.v.), cách tôi sử dụng nó hơi khác một chút và dễ dàng hơn nhiều — điều này có nghĩa là nó cũng dễ giải mã hơn . Dù sao, đây là cách tôi sử dụng nó:
Đầu tiên, viết các cặp chữ số tương ứng tương ứng với các chữ cái của nó: đầu tiên là số của dòng, sau đó là số của cột:
12 11 45 45 11 32 11
Sau đó, nhóm các chữ số đó thành một chuỗi liên tục:
12114545113211
Sau đó, chia đôi chuỗi đó, chia thành hai chuỗi:

Ví dụ: nếu chúng tôi muốn mã hóa từ “NGÔN NGỮ” bằng kỹ thuật này, nó sẽ tương ứng với “EPCJ5PJL” . Tuy nhiên, xin lưu ý rằng các mật mã thay thế như thế này rất dễ bị bẻ khóa bằng cách sử dụng phân tích tần suất, vì vậy hãy đảm bảo rằng tin nhắn được mã hóa của bạn không thể bị phá bởi những người không phù hợp . Trong hầu hết các trường hợp, lớp mã hóa thứ hai sẽ đảm bảo rằng thông điệp chắc chắn sẽ khó giải mã hơn.
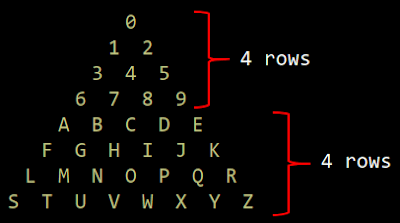
“Mỗi bàn tay bình thường của con người có thể được cho là có sáu vị trí rõ ràng; một nắm tay, một ngón tay (hoặc ngón tay cái) mở rộng, hai, ba, bốn và sau đó là cả năm. Nếu bàn tay phải được sử dụng để biểu thị một đơn vị, và còn lại để biểu thị “số sáu”, một người có thể biểu thị các giá trị từ 0 đến 55 senary (35 thập phân ) bằng ngón tay của họ, thay vì 10 thông thường thu được khi đếm ngón tay tiêu chuẩn. ví dụ: nếu ba ngón tay được mở rộng trên tay trái và bốn ở bên phải, 34 senary được đại diện. Điều này tương đương với 3 × 6 + 4 , là 22 thập phân .”
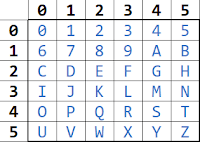
Sử dụng bảng này làm tài liệu tham khảo và xem xét rằng các dòng tương ứng với các ngón tay trên bàn tay trái và các cột tương ứng với các ngón tay trên bàn tay phải, chúng ta có thể biểu thị chữ “A” (dòng 1, cột 4) bằng cách giơ 1 ngón tay lên của bàn tay trái và 4 ngón tay của bàn tay phải. Tương tự như vậy, chữ “Z” (dòng 5, cột 5) sẽ được biểu thị bằng tất cả mười ngón tay giơ lên. Khi đó, số không sẽ được thể hiện bằng nắm tay khép lại (nghĩa đen là không có ngón tay nào giơ lên). Về mặt thực tế, điều này sẽ tương tự như mật mã thay thế bằng mật mã , trong trường hợp này sử dụng ký hiệu Base-6 làm tham chiếu.
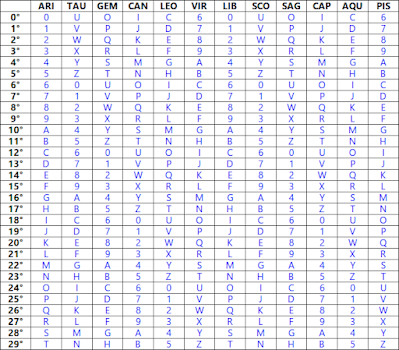
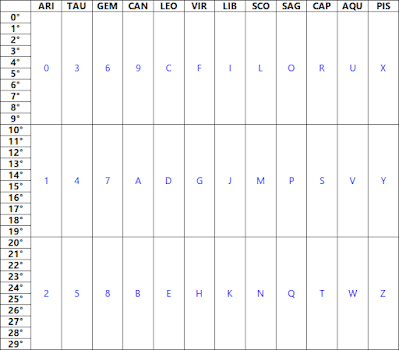
Vì vậy, về cơ bản, những gì chúng ta có ở đây là hai chuỗi chữ và số cuối cùng mã hóa ngày sinh của Aleister Crowley , bằng cách liên kết mỗi độ và decan với một chữ số cụ thể. Và điều này là như vậy bởi vì mỗi độ của cung hoàng đạo tương ứng với một sự kết hợp độc đáo của các ký tự cho decan và độ; không có bất kỳ hai độ nào chia sẻ cùng một cặp ký tự chữ và số, sử dụng phương pháp này.
Trong trường hợp của Crowley, hai chuỗi đó là:
- JZMKTLVD35 cho decan;
- và JS7O41VVVH cho cấp độ;
Điểm trừ duy nhất của phương pháp này là nó chỉ tính đến độ, không tính đến phút và giây của cung — nên thất bại thảm hại khi nói đến chi tiết .
Một cách để giải quyết vấn đề này là giữ nguyên cách chia cung hoàng đạo thành 36 phần bằng nhau (Decans) và sau đó chia nhỏ mỗi Decan thành 36 phần bằng nhau , với mỗi phần nhỏ hơn tương ứng với 16’40” (16 phút 40 giây của cung), do đó về mặt kỹ thuật chia Hoàng đạo thành 1296 hoặc 36 × 36 phần bằng nhau. Bằng cách đó, chúng tôi sẽ chỉ cần hai ký tự chữ và số để xác định từng phần nhỏ của 16’40”, bắt đầu từ 00 (0°00’00” đến 0°16’39” Aries) và kết thúc tại ZZ (29°13 ’20” đến 29°59’59” Song Ngư) . Phương pháp này có ưu điểm là sử dụng cùng một lượng ký tự chữ và số như phương pháp trước, đồng thời cho phép chi tiết hơn khi nói đến vị trí của các hành tinh.
Sự mặc khải của AQ trong bối cảnh của Thelema
Độc giả của tôi sẽ nhớ loạt bài tôi viết về mật mã Thelemic (phần I , II , III và IV ), và tôi phải nói rằng trong một thời gian rất dài, tôi đã rất thích thú với tiếng Anh Qaballa (mật mã “ALW”, được khám phá trong Phần I) và cách nó mang lại một số kết quả nổi bật ( khi so sánh với các mật mã Thelemic khác)khi nó được áp dụng choLiber AL vel Legis, Sách Luật.
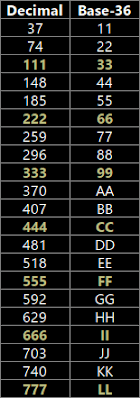
AQ là một nhánh của ký hiệu Base-36, có nghĩa là nó bao gồm chính xác 36 ký tự chữ và số (10 chữ số Ả Rập và 26 chữ cái tiếng Anh) có thể được sử dụng làm chữ số trong hệ thống số Base-36. Việc Aleister Crowley tự gọi mình là “Quái vật vĩ đại 666” và 666 là số tam giác 36ᵗʰ, chỉ cho thấy mối liên hệ có thể có này;
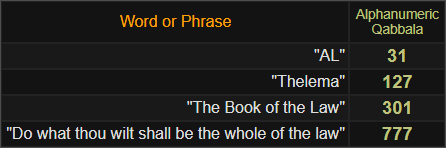
“AL” = 31
(“AL” là một công thức quan trọng trong Thelema, là một phần trong tên của Sách Luật. Crowley đã viết như sau: “” AL” là tên thật của Sách, đối với các chữ cái này và số 31 của chúng, mẫu Chìa khóa Chủ cho những Bí ẩn của nó.” —nguồn. Ngay cả khi xem xét rằng Crowley đang đề cập đến giá trị của “AL” trong tiếng Do Thái Gematria và tiếng Hy Lạp Isopsephy, điều khá đáng chú ý là công thức này thêm vào cùng một giá trị trong Chữ và số Qabbala.)
- “Thelema” = 127 (số nguyên tố thứ 31 ˢᵗ) = “Số”
- “Sách Luật” = 301
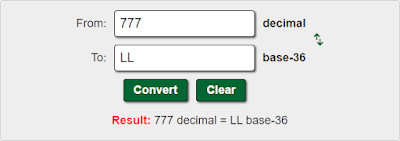
- “Làm gì thì làm theo luật” = 777
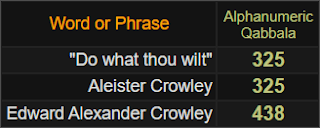
“Làm gì thì làm” = 325 = “Aleister Crowley”
– Tên khai sinh đầy đủ của Aleister Crowley là “Edward Alexander Crowley” , có tổng là 438 trong Alphanumeric Qabbala. Xét rằng 36 là số tam giác 8 ᵗʰ và 666 là 36 ᵗʰ, nên khá tò mò khi lưu ý rằng số (thập phân) 438 được viết là 666 trong ký hiệu Bát phân (cơ số 8 ).
“Làm gì thì làm” = 325 = “Aleister Crowley”
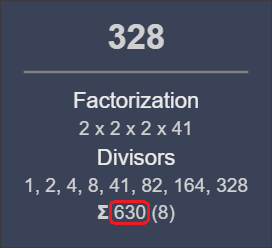
Có một số tương ứng thú vị khác mà người ta có thể tìm thấy khi sử dụng AQ trong ngữ cảnh của Thelema, mặc dù — và điều này rất quan trọng — nhiều mật mã khác nhau có thể mang lại kết quả gây tò mò như nhau, do đó, việc sử dụng các số khớp để chứng minh quan điểm của chúng ta có thể không phải lúc nào cũng phù hợp. sự lựa chọn tốt nhất. Dù sao đi nữa… trong các bài kiểm tra của tôi với mật mã này khi nghiên cứu Luật thư, tôi đã tìm kiếm các giá trị của các từ, tên, cụm từ cụ thể và cả câu thơ, và tôi nhận thấy rằng chỉ có hai câu thơ hoàn chỉnh cộng lại thành 630 — tổng của tất cả các số từ 0 đến 35:
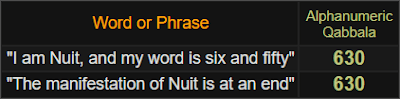
Từ “biểu hiện” chỉ xuất hiện một lần nữa trong câu đầu tiên của Liber AL:

Nhưng có một điều nữa mà tôi muốn nói vào lúc này. Tất cả các mật mã đã được điều chỉnh hoặc phát triển để sử dụng trong ngữ cảnh của Thelema đã được áp dụng cho một số câu đố quan trọng trong Luật thư , cụ thể là AL II:76 và AL III:47, để xác minh “tính hợp lệ” của chúng . Và khi tôi đang đề xuất Alphanumeric Qabbala để giải mã Sách Luật, bây giờ tôi sẽ đưa ra giải pháp của riêng mình cho câu đố có lẽ được biết đến rộng rãi nhất trong Sách Luật.
Lưu ý cẩn thận:
Thỉnh thoảng (có thể là “hồi đó” nhiều hơn bây giờ) , một “Thelemic English Qabalah” mới đột nhiên xuất hiện, với một người nào đó tuyên bố đã tìm thấy chiếc chìa khóa được hứa hẹn sẽ giải quyết mọi bí ẩn của Sách Luật. Mặc dù tôi thích một số ý tưởng đằng sau một số hệ thống này — đặc biệt là những hệ thống mà tôi đã viết nhiều nhất — nhưng tôi không tránh khỏi cảm giác khó chịu khi đề xuất mật mã này như một chìa khóa quan trọng của Thelema, đơn giản vì tôi không muốn lặp lại cùng một lịch sử đã được viết và viết lại bởi những người khác.
Đây là những câu thơ trong câu hỏi:
Có thể nói “lời giải” này không “có ý nghĩa” gì đối với tôi, ngoại trừ việc “câu đố” không bao giờ được coi là nghiêm túc. Không có nghĩa là số hoặc chữ cái nào được sử dụng trong đó — mà thực tế là chúng được sử dụng như thế nào .
Bốn lần cùng một thông điệp được lặp lại:
“24 89 RPSTOVA L”
Và thông điệp sẽ là: Các chữ cái luôn xuất hiện sau các con số – đó chính xác là đặc điểm cơ bản nhất của Alphanumeric Qabbala. Và do đó, câu trả lời có thể thu được, giả sử rằng Alphanumeric Qabbala là “chìa khóa” dự định để giải mã AL.
(Các chữ cái đến sau “số” – tức là các chữ số.)

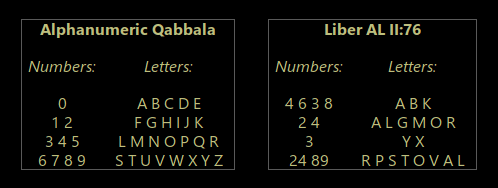

- Luật Thelema, “Hãy làm những gì bạn muốn sẽ là toàn bộ luật pháp” tổng hợp 777 trong Qabbala chữ và số.Sau đó, hãy xem xét rằng trong cuốn sách về số và chữ cái của Crowley , Liber 777 , Crowley đã liệt kê mười sephiroth đánh số chúng từ 1 đến 10, và sau đó là 22 chữ cái tiếng Do Thái (“đường đi”), đánh số chúng từ 11 (Aleph) đến 32 (Tav).
Nếu chúng ta điều chỉnh hệ thống đó cho phù hợp với Bảng chữ cái tiếng Anh, liệt kê đầu tiên mười chữ số Ả Rập từ 0 đến 9, sau đó là 26 chữ cái tiếng Anh từ A đến Z, thì chúng ta sẽ kết thúc chính xác với Alphanumeric Qabbala: một liên tục, hợp lý và dãy chữ số không dư thừa từ 0 đến Z=35.
Tôi không đưa ra tuyên bố nào về “vai trò của mình” trong giải pháp này, vì tôi nghĩ điều đó không liên quan – ý định của tôi không phải là khẳng định rằng tôi đã tìm thấy “Chìa khóa của tất cả” hay rằng tôi là “đứa con của Quái vật”. Theo tôi, điều đó đơn giản là ngu ngốc và non nớt, và sẽ không dẫn bạn (hoặc tôi, hoặc bất kỳ ai) đến bất cứ đâu. Tuy nhiên, tôi tin rằng AQ có thể là chìa khóa quan trọng trong Thelema, và những gì tôi đang làm ở đây chỉ đơn giản là chơi cùng với nó và cố gắng làm cho nó được biết đến rộng rãi hơn.
Tất nhiên, tất cả những điều này không thể được coi là “bằng chứng” rằng Alphanumeric Qabbala là chìa khóa quan trọng đối với Thelema – thứ nhất, bởi vì nhiều trận đấu trong số này có thể được coi là ngẫu nhiên và tôi nghĩ rằng hầu hết các nhà đá quý sẽ đồng ý với tôi về kết luận này. Và thứ hai, bởi vì vẫn còn nhiều việc phải làm trong lĩnh vực này, đồng thời việc liên tục đề xuất quá nhiều mật mã để giải mã những bí ẩn của Liber AL đã khiến chủ đề này trở thành một loại “cấm kỵ” trong bối cảnh của Thelema. Vì vậy, những gì tôi đang cố gắng đạt được bằng cách viết bài này, trên thực tế, là để trình bày một số ý tưởng và sau đó để Độc giả của tôi tự làm phần còn lại. Tất nhiên, tôi luôn quan tâm đến việc trao đổi ý kiến về Gematria, và về chủ đề này nói riêng – vì vậy, nếu bạn, Độc giả thân mến, cảm thấy cần liên lạc và thảo luận về một số điều này, vui lòng làm như vậy !
“Nên” và “không nên” với AQ
Trong phần này, tôi sẽ cố gắng giải thích cách cá nhân tôi sử dụng Chữ và số Qabbala, điều này sẽ được phản ánh qua các đề xuất của tôi về “nên” và “không nên” liên quan đến công việc với AQ.
Trước hết, hãy bắt đầu với những gợi ý của tôi cho “dos” :
- Sử dụng AQ bất cứ khi nào thấy hợp lý khi sử dụng mật mã chữ và số , ví dụ: trong các cụm từ hoặc chuỗi bao gồm các chữ số (0-9) và chữ cái (AZ).
- Sử dụng AQ với ngôn ngữ tiếng Anh ! Bên cạnh các mật mã Tiêu chuẩn , Thứ tự và Rút gọn mà tôi xem là các mật mã chính của tiếng Anh — việc sử dụng AQ cho các từ, cụm từ hoặc thuật ngữ cụ thể trong tiếng Anh cũng rất có ý nghĩa, vì nó hoàn toàn phù hợp với chuỗi chữ và số bao gồm 10 chữ số Ả Rập (từ 0 đến 9) và 26 chữ cái tiếng Anh (từ A đến Z).
- Sử dụng AQ trong ngữ cảnh của Thelema (!!!). Công việc với AQ trong lĩnh vực này cực kỳ khan hiếm , ngoài một số khám phá không thường xuyên được chia sẻ ở đây và ở đó bởi một số (rất ít) người, vì vậy tôi nghĩ đã đến lúc phải thực hiện một số công việc nghiêm túc với mật mã này trong nghiên cứu về Thánh thư của Thelema — Liber AL vel Legis mới chỉ là bước khởi đầu.
- Sử dụng AQ để mã hóa các tham chiếu ẩn trong văn bản của bạn ! Trên thực tế, đó là một trong những cách sử dụng Gematria yêu thích của tôi. Bạn cũng có thể làm điều này và có thể dễ hoặc khó tùy thuộc vào công cụ bạn sử dụng. Tôi khuyên bạn nên sử dụng Gematro , bao gồm công cụ “Mã hóa” cũng như liên kết đến danh sách cơ sở dữ liệu công khai ngày càng tăng (kiểm tra menu “Giới thiệu”) — nó sẽ giúp công việc của bạn dễ dàng hơn rất nhiều và sẽ cho bạn hàng giờ đảm bảo vui vẻ.
- Không sử dụng AQ bất cứ khi nào sử dụng nó KHÔNG hợp lý , điều này khá rõ ràng, mặc dù cần có một lời giải thích ngắn gọn. Ví dụ, tôi sẽ không bao giờ sử dụng AQ để cố gắng “giải mã” một văn bản viết bằng tiếng Latinh hoặc tiếng Anh thời Elizabeth, vì lý do đơn giản là bảng chữ cái được sử dụng cho những ngôn ngữ này khác với tiếng Anh hiện đại. AQ, và các mối liên hệ phức tạp của nó với số 36, chỉ có ý nghĩa khi được sử dụng với (1) hệ đếm thập phân (0 đến 9) kết hợp với (2) bảng chữ cái tiếng Anh hiện đại gồm 26 chữ cái.
- Đừng cố giải mã bất kỳ tên hoặc cụm từ ngẫu nhiên nào bằng AQ — hoặc bằng bất kỳ mật mã nào khác, trên thực tế! Chúng ta luôn cần hết sức cẩn thận khi “giải mã” thứ gì đó, đặc biệt nếu chúng ta không chắc chắn rằng nó đã được mã hóa ngay từ đầu. Vì vậy, những thứ như tìm kiếm các mẫu trong ngôn ngữ tiếng Anh trong khi sử dụng AQ có thể hiệu quả hoặc không, tùy thuộc vào những gì bạn muốn làm với nó. Nếu bạn chỉ đơn giản là tìm kiếm các mẫu, tôi có thể đảm bảo rằng bạn sẽ tìm thấy chúng — cho dù với chữ và số Qabbala, tiếng Anh thông thường hay tiêu chuẩn, tiếng Anh Qaballa hay mật mã Latinh của Agrippa. Câu hỏi thực tế là một số khớp thực sự “có nghĩa là” -và nó chỉ có nghĩa là những gì bạn muốn nó có nghĩa. Ví dụ: một số cách giải thích “thay thế” về Kinh thánh bắt đầu bằng cách phân tích nó bằng tiếng Do Thái Gematria (và tiếng Hy Lạp Isopsephy) và thiết lập mối liên hệ giữa các từ và khái niệm dựa trên các số trùng khớp và/hoặc các mẫu hình học. Vì vậy, một kết hợp số là một phương tiện mã hóa (không chỉ giải mã ) một cái gì đó và đôi khi nó có thể cung cấp cho bạn một số ý tưởng tuyệt vời. Nhưng đừng lạm dụng tìm kiếm các mẫu và kết hợp để tìm kiếm “bằng chứng” về điều gì đó. Các kết quả trùng khớp về bản chất không chứng minh được điều gì — nhưng chúng có thể là một cách thông minh để nói nhiều hơn những gì bạn thực sự đang nói.
Và cuối cùng nhưng không kém phần quan trọng (whew!) …
Câu đố – và một số ghi chú về văn bản này
Một trong những cách sử dụng Gematria yêu thích của tôi là mã hóa các tham chiếu bí mật trong văn bản của tôi. Và vì vậy, vì chủ đề chính của blog của tôi là Gematria, trong văn bản này, tôi đã mạn phép để lại một số “mẩu tin lưu niệm” hoặc các tài liệu tham khảo ẩn trong suốt bài viết, để những Người đọc nhạy cảm nhất của tôi sẽ hiểu, trên thực tế, một trong những cách làm thế nào.
Tôi làm việc với Gematria.
- tất cả văn bản có màu đều được mã hóa;
- đôi khi, các cụm từ có định dạng khác cũng có thể ẩn một số tham chiếu.
Để biết liệu thứ gì đó có được mã hóa có mục đích hay không, một trong những điểm quan trọng khi làm việc với Gematria để “giải mã” thứ gì đó, hãy nhớ những điều sau: nếu nó trông quá đẹp để có thể là ngẫu nhiên, thì có thể nó không phải là ngẫu nhiên . Tuy nhiên, để chắc chắn về điều này, chúng tôi luôn phải xác nhận những phát hiện của mình bằng cách lưu ý (1) bối cảnh chúng tôi đang làm việc và (2) liệu các mật mã chúng tôi đang sử dụng có hợp lý để sử dụng trong bối cảnh đó hay không.
Vì vậy, trong bối cảnh cụ thể này, mật mã chính bạn cần sử dụng là Alphanumeric Qabbala… và có thể là 2 hoặc 3 mật mã nữa trong một số trường hợp. Dù sao đi nữa, nếu bạn không biết, hãy nhớ làm quen với Gematro , một trong những máy tính Gematria tốt nhất hiện có, để cả hai cùng giải mã và mã hóa bất cứ thứ gì bạn muốn trong văn bản của mình. Nó sẽ làm cho công việc của bạn dễ dàng hơn rất nhiều.
Cảm ơn vì đã theo dõi công việc của tôi và… hãy tiếp tục giải mã!
Tác giả: Luís Gonçalves
Biên Dịch: Hiển Nguyễn Kabala