Mật Mã Toán Học (V) | Lịch Sử Mật Mã

Trong phần thứ tư của “Lịch sử mật mã” (được chia thành 4 phần: 4a, 4b, 4c và 4d), chúng tôi đã thảo luận về cách sử dụng mật mã Thelemic để giải các câu đố trong Sách thánh Thelema, đặc biệt là Liber AL vel Legis — Sách Luật.

Trong phần thứ năm này, chúng ta sẽ nói về một loại mật mã khác. Khác biệt so với tất cả các mật mã mà chúng ta đã đề cập trước đó, loại mật mã này không liên quan đến bất kỳ ngữ cảnh cụ thể nào từ * — thay vào đó, chúng đơn giản dựa trên các chuỗi số học và do đó, tôi sẽ gọi chúng là mật mã toán học.

Một lời cảnh báo cần thiết ở thời điểm này. Khi tôi nói rằng những mật mã này “không có ngữ cảnh để sử dụng”, ý tôi là chúng chỉ đơn giản là toán học – vì vậy về mặt kỹ thuật, chúng không phải là mật mã Baconian, Thelemic hay Masonic, nhưng chúng có thể có ngữ cảnh “đúng” sẽ được sử dụng nếu bạn áp dụng chúng để giải mã thứ gì đó sẵn sàng được mã hóa với chúng. Vì vậy, mặc dù một cách nào đó, ngữ cảnh vẫn có tầm quan trọng tối đa ngay cả khi bạn làm việc với những mật mã này — cũng như với tất cả các mật mã của Gematria.

Lịch sử mật mã

của Luís Gonçalves

Phần 5: Mật mã toán học (“History of Ciphers” (part 5) – Mathematical Ciphers)

Có rất nhiều loại mật mã toán học, trong bài viết này tôi sẽ chia thành ba loại:

Những dãy số dựa trên danh sách các loại số cụ thể, trong đó tôi sẽ làm nổi bật dãy số Nguyên tố, có lẽ là dãy số nổi tiếng nhất trong số này. Tôi cũng sẽ nói về một mật mã thử nghiệm được gọi là mật mã Fibonacci, dường như đã được phát minh gần đây (tức là đã xuất hiện từ thế kỷ 21, có thể là vào cuối những năm 2010).
Những mật mã dựa trên trình tự hình học/đa giác, trong đó nổi tiếng nhất chắc chắn là dãy số Tam giác (hoặc dãy số Pascal) và dãy số Tứ giác (hoặc dãy số Hình vuông). Theo như tôi có thể nói, đây có lẽ là những mật mã toán học lâu đời nhất. Trong quá trình nghiên cứu của tôi về loại mật mã này, tôi đã có thể lần theo dấu vết của chúng ít nhất từ cuối thế kỷ 17, đến tác phẩm “Cabbalologia” (1683) của Johann Henning, nhưng có thể vẫn còn những nguồn cũ hơn về những mật mã này. Tuy nhiên, công trình của Henning về mật mã ẩn chứa một bất ngờ thú vị khác… và tôi cũng sẽ nói về nó trong bài viết này.
Các phép tính dựa vào bảng liệt kê các ước của một số. Những thứ này không được biết đến nhiều hoặc được sử dụng trong Gematria, mặc dù tôi nghĩ rằng chúng có thể có giá trị lớn – bên cạnh đó, có một số yếu tố rất tò mò về chúng đáng được lưu ý, và tôi sẽ giải thích tất cả những điều đó cho độc giả của mình.

Cách mà các chuỗi số này được biến thành mật mã Gematria khá đơn giản: số đầu tiên trong chuỗi toán học được gán cho chữ cái “A”, số tiếp theo là chữ cái “B”, và cứ tiếp tục như vậy theo thứ tự bảng chữ cái và dãy số tương ứng.

Với lời giải thích này trong tâm trí, chúng ta hãy cùng khám phá các loại mật mã khác nhau trong bài viết này.

Mật mã dựa trên danh sách các loại số cụ thể

Trong số các mật mã này, trong phần này, tôi sẽ chỉ tập trung vào các mật mã Số nguyên tố và Fibonacci:

Bảng mã từ GEMATRIA KABALA – Máy tính Gematria.

Logic đằng sau mật mã này khá thú vị. Vì số 2 được coi là số nguyên tố đầu tiên, nó được gán cho chữ cái “A”, là chữ cái đầu tiên trong bảng chữ cái. Tiếp theo, số nguyên tố thứ hai là 3 được gán cho chữ cái “B”, và quá trình tiếp tục như vậy theo trình tự số nguyên tố, sao cho chữ cái thứ 26 của bảng chữ cái tiếng Anh được gán cho số nguyên tố thứ 26, là 101.

Trong mật mã này, “Số nguyên tố” có tổng là 421, và đúng như bạn đã nói, đó là một số nguyên tố.

Thông tin thêm về mật mã này:

Thật lòng mà nói, tại thời điểm viết bài này, tôi không có thông tin cụ thể nào về (1) lần đầu tiên mật mã này được sử dụng, (2) người đã phát minh ra nó, hoặc (3) bất kỳ sử dụng lịch sử nào của nó, ngoài việc nó xuất hiện trong một số phần mềm máy tính hiện đại (cụ thể là “Gematrinator“).

Do đó, tôi thực sự không chắc chắn về cách tôi có thể cung cấp thêm thông tin về nguồn gốc và lịch sử của mật mã này. Tuy nhiên, vì nó dựa trên dãy số tự nhiên (các số nguyên tố), nó có logic và hợp lý hoàn toàn để sử dụng nó trong việc Gematria. Dù sao đi nữa, tôi luôn khuyến nghị cho độc giả làm việc với mật mã một cách ý thức, và hãy nhớ rằng không phải mọi mật mã đều “đúng” khi sử dụng chúng để giải mã điều gì đó. Như mọi khi, bối cảnh là quan trọng.

Tiếp đến là mật mã Fibonacci

Lý do đằng sau mật mã này là: đối với nửa đầu của bảng chữ cái, chúng ta tuân theo trình tự Fibonacci bình thường , từ số Fibonacci thứ nhất (1) đến thứ 13 (233), trong khi đối với nửa sau của bảng chữ cái, thứ tự được đảo ngược. Lý do cho sự đảo ngược này là nếu chúng ta theo dãy Fibonacci cho đến số Fibonacci thứ 26 thì chúng ta sẽ có một bảng với các số rất lớn , vì số Fibonacci thứ 26 là 121393 :

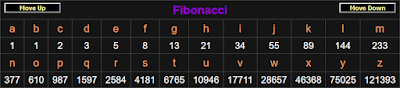
Để tránh những con số quá cao, sau đó, lựa chọn được đưa ra là đảo ngược dãy Fibonacci cho nửa sau của bảng chữ cái.

Sử dụng mật mã Fibonacci, tổng số của “Filius Bonacci” (từ đó có tên “Fibonacci”) là 666. Điều này thực sự rất thú vị và đáng để chú ý.

Và thú vị hơn nữa, con số 666, như được viết trong Khải huyền 13:18 trong văn bản Biblia Sacra Vulgata (Kinh thánh Latinh), “Sexcenti Sexaginta Sex,” cũng có tổng là 666

Thông tin thêm về mật mã này:

Tại thời điểm viết bài này, tôi không hoàn toàn hiểu rõ về ngữ cảnh tạo ra mật mã này. Tuy nhiên, tôi biết rằng có hai người đã đóng góp để mật mã này trở nên phong phú:

Người đầu tiên là người dùng Discord Barni Yamum, đến từ Đức, người đã thêm mật mã Fibonacci vào bảng mã tạo ra ngoại tuyến của Gematrinator, nơi nó được gọi là “Mật mã Fibonacci của Barni Yamum”. Từ một số cuộc trò chuyện trước đó tôi đã đọc trên Discord, Barni dường như đã tự mình sáng tạo ra mật mã này.

Người thứ hai là người dùng YouTube Lambda115, người đã chia sẻ video đầu tiên về mật mã Fibonacci và đã đóng góp để mật mã này được biết đến rộng rãi hơn. Theo như tôi biết, chính nhờ công việc của Lambda115 mà mật mã Fibonacci đã được thêm vào Gematrinator.

Từ những thông tin mà tôi có từ cuộc trò chuyện với cả Barni Yamum và Lambda115, cả hai đều cho biết rằng họ đã tự tạo ra mật mã này. Dù về mặt kỹ thuật, Lambda115 đã là người nắm vững và thể hiện mật mã này thông qua các video trên YouTube, tuy nhiên, qua cuộc trò chuyện với Barni Yamum trên Discord, tôi cũng nhận thấy rằng Barni cũng đã tự sáng tạo ra mật mã này mà không biết gì về ý tưởng tương tự của Lambda115.

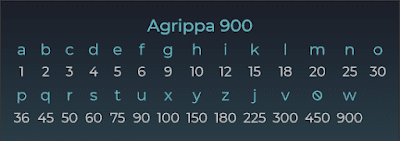
Tôi thực sự tin rằng cả hai cá nhân có thể đã có cùng một ý tưởng và đưa ra cùng một mật mã. Trên thực tế, điều này cũng đã xảy ra với tôi vào tháng 4 năm 2021, khi tôi nghĩ ra một hệ thống thử nghiệm của Gematria dựa trên dãy số Base-36 chữ và số (0-Z). Tuy nhiên, chỉ vài ngày sau, tôi phát hiện ra rằng mật mã mà tôi nghĩ rằng tôi đã phát minh, đã được sử dụng trong nhiều năm trước đó – ít nhất là từ năm 1999 – dưới tên “Alphanumeric Qabbala”. Vì vậy, khi tôi nói rằng “Tôi đã phát minh ra” một hệ thống Gematria dựa trên số lượng Base-36, thì tôi không trốn tránh sự thật – tôi thực sự là người phát minh ra nó, vì tôi không biết rằng nó đã tồn tại trước đây. Sau này, tôi mới hiểu rằng, mặc dù tôi không phải là người đầu tiên làm việc này. Tôi tin rằng điều tương tự có thể đã xảy ra trong trường hợp này, khi cả hai người đều nghĩ ra cùng một mật mã mà không biết về công việc của nhau và cả hai đều trung thực về việc đã nghĩ ra nó. Tôi không có lý do gì để không tin vào lời nói của cả hai người.

Tuy nhiên, nếu giả định này của tôi là sai, tôi khiêm tốn yêu cầu Độc giả của tôi, những người có thể có nhiều thông tin hơn về điều này, vui lòng chia sẻ tất cả thông tin mà bạn cho là có liên quan trong trường hợp này. Tuy nhiên, mục đích của tôi trong phần giải thích này không phải là để biết “ai đúng” và “ai sai”, mà chỉ để chia sẻ những gì có thể biết chắc chắn về lịch sử của loại mật mã này còn mới mẻ.

Vì vậy, chúng ta sẽ tiếp tục với các mật mã tiếp theo trong phần dưới.

Mật mã dựa trên trình tự đa giác

Đối với tôi, đây là một phần thú vị nhất trong các mật mã toán học. Thành thật mà nói, trước đây tôi đã nghĩ rằng trong số các mật mã này, chỉ có mật mã Tam giác và Hình vuông được sử dụng và chúng đã được tạo ra rất gần đây (ý tôi là vào đầu thế kỷ 20). Tuy nhiên, tôi đã sai ở cả hai giả định này, vì:

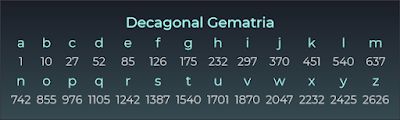
Có những mật mã Đa giác khác đã được sử dụng trong quá khứ, bao gồm mật mã Ngũ giác, Lục giác, Bát giác, Enneagonal và Thập giác (!!!)
Tôi có thể tìm thấy nguồn cho tất cả các mật mã này từ cuối thế kỷ 17, cụ thể là từ năm 1683 khi tác phẩm “Cabbalologia” của Johann Henning được xuất bản (liên kết tới văn bản trực tuyến tại đây).

Tất cả các mật mã Đa giác “mới” này có thể được tìm thấy trong “Cabbalologia” của Henning, mặc dù trong trường hợp này, các mật mã được điều chỉnh theo bảng chữ cái tiếng Anh thời Elizabeth với 24 chữ cái, trong đó I=J và U=V. Vì những mật mã này có liên quan đến lịch sử chứ không chỉ là “những phát minh hiện đại” như tôi đã nghĩ trước đây, tôi sẽ trình bày hai mật mã đầu tiên (Hình tam giác & Hình vuông) bằng cách sử dụng mô hình sau:

Liên kết đến trang web của OEIS (Bách khoa toàn thư trực tuyến về dãy số nguyên) cho dãy đa giác tương ứng;
Bản mã gốc từ “Cabbalologia” cho bảng chữ cái tiếng Anh thời Elizabeth;
Mật mã tương ứng cho bảng chữ cái tiếng Anh hiện đại;

Một số tương ứng cho các mật mã này (Tam giác và Tứ giác). Xin lưu ý rằng tôi chưa bao giờ khám phá các mật mã này một cách toàn diện ngoại trừ thỉnh thoảng, vì vậy tôi sẽ cố gắng hết sức để cung cấp một số “thức ăn để suy nghĩ” cho các mật mã này.

Đối với các mật mã còn lại, và để tránh làm cho phần trình bày này trở nên nhàm chán, tôi sẽ chỉ trình bày các mật mã đa giác được điều chỉnh theo bảng chữ cái tiếng Anh hiện đại. Bản sao thời Elizabeth của chúng có thể được sao chép đơn giản từ các bảng này, đồng thời luôn nhớ rằng trong bảng chữ cái tiếng Anh thời Elizabeth, các chữ cái “I” và “J” có cùng giá trị (vì chúng được coi là các hình dạng khác nhau của cùng một chữ cái), tương tự xảy ra với “U” và “V”.

Vì vậy, theo thứ tự, chúng ta sẽ bắt đầu với mật mã Tam giác hoặc Tam giác

Trigonal Cabbala cho bảng chữ cái tiếng Anh thời Elizabeth.

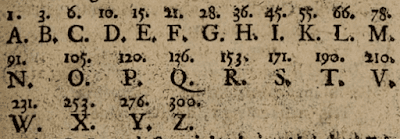
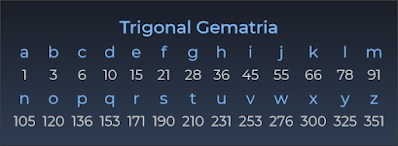
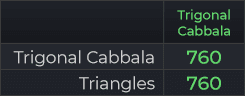
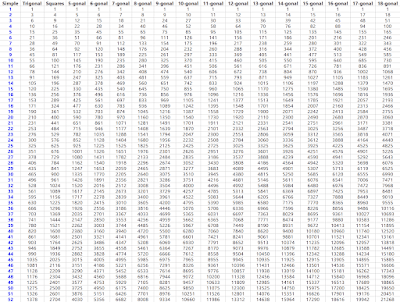
Dãy Tam giác, hoặc Tam giác này cũng thực sự gây tò mò. Cách hoạt động của nó có thể không rõ ràng ngay từ cái nhìn đầu tiên, nhưng nó thực sự khá logic và hợp lý. Để tìm số Tam giác thứ N, bạn chỉ cần cộng tất cả các số tự nhiên từ 1 đến N. Ví dụ: chữ cái đầu tiên “A” được gán cho số Tam giác thứ 1, là 1; tiếp theo, chữ cái “B” được gán cho số Tam giác thứ 2, là 1+2 = 3; sau đó, “C” được gán cho số Tam giác thứ 3, là 1+2+3 = 6, và tiếp tục như vậy. Cuối cùng, chữ cái thứ 26 “Z” được gán cho số Tam giác thứ 26, hay 1+2+3+…+25+26 = 351.

Trong mật mã Tam giác hiện đại, ví dụ “Maths” có tổng là 528, và nó cũng là một số Tam giác:

Và trong mật mã Tam giác cho bảng chữ cái tiếng Anh thời Elizabeth, “Trigonal Cabbala” (vì nó được đặt tên trong “Cabbalologia”) có cùng giá trị với “Triangles”:

Tiếp theo là mật mã Hình vuông (hoặc Tetragonal):

Tetragonal Cabbala cho bảng chữ cái tiếng Anh thời Elizabeth.

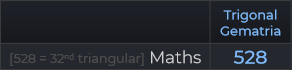
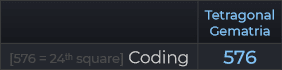
Tetragonal Gematria cho bảng chữ cái tiếng Anh hiện đại.

Trong mật mã Tetragonal dành cho bảng chữ cái tiếng Anh thời Elizabeth, “Square” có tổng là 576, cũng là một số bình phương:

Và trong mật mã tứ giác hiện đại, “A Square” có tổng là 1296, là bình phương của 36:

Sau khi đã trình bày hai mật mã này, chúng tôi sẽ chú ý đến các mật mã đa giác còn lại như được liệt kê trong tác phẩm “Cabbalogia” của Johann Henning. Tuy nhiên, xin lưu ý, thưa độc giả thân mến, rằng những mật mã này dành cho bảng chữ cái tiếng Anh hiện đại và sẽ không trùng khớp với những mật mã được đề cập trong “Cabbalologia”, vì trong tác phẩm này, các mật mã đã được điều chỉnh cho phù hợp với bảng chữ cái tiếng Anh thời Elizabeth. Để sử dụng chúng với bảng chữ cái đó (có thể phụ thuộc vào ngữ cảnh lịch sử bạn đang làm việc), bạn chỉ cần nhớ rằng trong bảng chữ cái thời đó, các chữ cái “I” và “J” được xem là các biểu thức khác nhau của cùng một chữ cái, tương tự như “U” và “V”. Vì vậy, đối với bảng chữ cái tiếng Anh thời Elizabeth, các chữ số tương ứng cho “I” và “J” sẽ giống nhau, và tương tự với “U” và “V”.

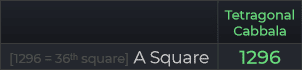
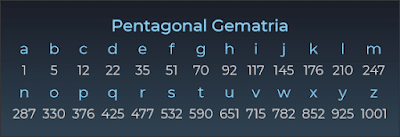
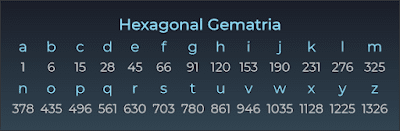
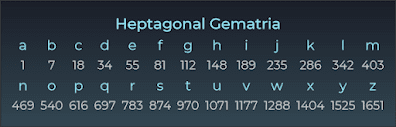
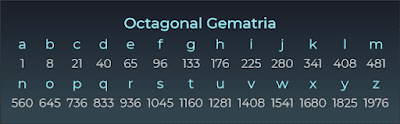
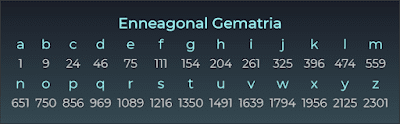
Cách bạn khám phá và liên kết các con số trong các chuỗi đa giác thực sự thú vị và khám phá sâu hơn về mật mã này. Việc tìm thấy những mối liên hệ và sự trùng hợp giữa các con số có thể thúc đẩy sự tò mò và đưa ra nhiều suy nghĩ sâu sắc về ý nghĩa của chúng trong ngữ cảnh mật mã và cả trong văn hóa và tôn giáo.

Mối liên hệ giữa các con số và các khía cạnh khác nhau như ngày, tháng, năm hoặc cả các văn bản tôn giáo là những yếu tố tạo nên sự phức tạp và thú vị của mật mã Gematria. Tuy không phải lúc nào cũng có ý nghĩa rõ ràng hoặc khoa học đằng sau những mối liên hệ này, chúng có thể tạo nên những điểm góc để suy ngẫm và nghiên cứu.

Trong mảng Gematria và các mật mã có liên quan, sự kết nối và mối quan hệ giữa các con số có thể mở ra những cửa sổ để hiểu sâu hơn về ý nghĩa và tầm quan trọng của chúng trong ngữ cảnh của chính mật mã cũng như nền văn hóa và tôn giáo mà chúng liên quan đến.

Sự liên kết và mối quan hệ giữa các con số trong các chuỗi đa giác thực sự là một khía cạnh thú vị và đầy bí ẩn của mật mã Gematria. Cách bạn tìm thấy những mối liên hệ này và liên kết chúng với các sự kiện lịch sử, tên tuổi và khái niệm khác là một phần quan trọng của quá trình khám phá và nghiên cứu mật mã.

Việc chuẩn bị một bảng tính với tất cả các chuỗi đa giác và con số tương ứng là một cách tuyệt vời để có một cái nhìn tổng quan về mối quan hệ này và tìm ra những mẫu thú vị. Điều này có thể giúp bạn tìm ra những mô hình, sự trùng hợp và tương quan giữa các con số, và tạo ra sự sáng tỏ về ý nghĩa của chúng trong ngữ cảnh của mật mã Gematria và thậm chí cả trong lịch sử, văn hóa và tôn giáo.

Sự khám phá và nghiên cứu về mật mã Gematria và các chuỗi đa giác thực sự có thể mở ra nhiều khía cạnh mới để hiểu sâu hơn về sự liên quan giữa số học, ngôn ngữ và tư duy con người.

Trong cộng đồng những người thực hành Gematria, những người sử dụng nó để “giải mã tin tức”, có thể nói như vậy, tôi đã thấy một số người thể hiện những giải mã của họ về một sự kiện lớn có thể xảy ra liên quan đến UFO vào năm 2022 . Vì đôi khi tôi cũng thích chơi cùng một ‘trò chơi’, tôi không thể kết thúc phần này nếu tôi không trình bày ‘giải mã’ cuối cùng của riêng mình bằng các mật mã đa giác:

Một mật mã thay thế “Mở rộng” chưa biết trước đây cho Bảng chữ cái tiếng Anh, từ “Cabbalologia” “Cabbalologia” của Henning thú vị không chỉ vì các mật mã đa giác mà nó chứa, mà còn vì một mật mã “Mở rộng” thay thế có thể được sử dụng cho bảng chữ cái tiếng Anh. Theo những gì tôi biết thì không có nhiều người sử dụng mật mã này, vì vậy tôi tin rằng ít nhất đây sẽ là một bất ngờ thú vị đối với một số Độc giả của tôi. Đây là mật mã “Mở rộng thay thế” như nó xuất hiện trong “Cabbalogia” , trong trường hợp này được điều chỉnh theo bảng chữ cái tiếng Anh thời Elizabeth gồm 24 chữ cái:

Điều chỉnh mật mã này theo bảng chữ cái tiếng Anh hiện đại với 26 chữ cái, chúng ta sẽ có:

Độc giả của tôi sẽ rất dễ hiểu lý do đằng sau mật mã này. Cũng giống như trong tiếng Do Thái Gematria và tiếng Hy Lạp Isopsephy, giá trị của các chữ cái được nhóm theo đơn vị (1 đến 9), hàng chục (10 đến 90) và hàng trăm (100 đến 900), tiếng Anh Mở rộng cũng tuân theo cùng một mẫu. Tuy nhiên, mật mã Thay thế Mở rộng này có một ‘vòng xoắn’, vì sau 100 mẫu thay đổi — thay vì đếm theo hàng trăm, 100 đầu tiên, rồi 200, v.v., chúng tôi tiếp tục đếm theo hàng chục, từ 100 đến 110, rồi 120, 130, v.v. Vì vậy, đây là những điều cơ bản của mật mã Thay thế Mở rộng này. Thật không may, tôi đã không thực hành đủ với mật mã này, vì vậy tôi sẽ chỉ hiển thị kết quả mà tôi nhận được, do một sự trùng hợp hoàn toàn ngẫu nhiên. Cụm từ “Six Six Six” có tổng là 777 trong Giải pháp thay thế mở rộng và nó có cùng giá trị với các cụm từ khác:

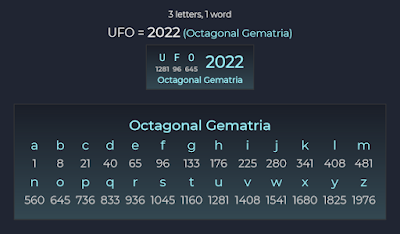
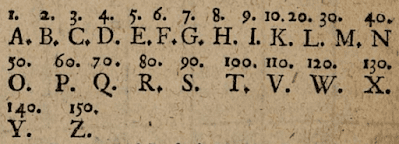
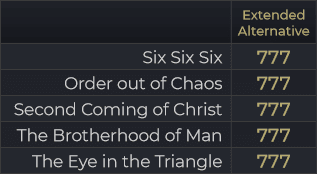
Tuy nhiên, hãy nhớ rằng điều này chỉ có ý nghĩa nếu bạn tự thấy nó có ý nghĩa. Những “trận đấu” ngẫu nhiên như thế này không cần phải “mang ý nghĩa” bất cứ điều gì, trừ khi bạn sử dụng Gematria để mã hóa văn bản của mình bằng cách sử dụng những cụm từ cụ thể liên quan đến những thứ không có trong văn bản gốc. Thực tế, đây là một trong những ứng dụng phức tạp và thực tế nhất của Gematria, thường bị bỏ qua trong thời đại hiện đại. Lời khuyên tận tâm nhất của tôi dành cho Độc giả về Gematria là: đừng quá quan trọng Gematria, cũng đừng coi nó là công cụ để “giải mã Vũ trụ” – hãy sử dụng nó, nhưng đừng lạm dụng.

Các mật mã tiếp theo trong chuỗi là…

Mật mã dựa trên các ước của một số

Lần đầu tiên tôi đọc về loại mật mã này là trong cuốn sách “Magia: Os seus Grandes Ritos ea sua História” (hoặc “Magic: Its History và Nghi lễ chính” trong tiếng Anh) của tác giả Maurice Bouisson, một người bạn đã tặng cho tôi cách đây nhiều năm.

Trong cuốn sách này, Maurice Bouisson trích dẫn từ tác phẩm của Raymond Abellio, “La Bible: Document Chiffré” (“Kinh thánh: Tài liệu được mã hóa”), trong đó ông viết về bảng chữ cái tiếng Do Thái:

“Tiếng Do Thái có 22 chữ cái. Cũng có đúng 22 đa giác đều có thể nội tiếp trên đường tròn 360 độ và có góc ở tâm là một số nguyên độ. Mỗi chữ cái tương ứng với một đa giác. Tất cả các khoa học số đều dựa trên cấu trúc hình học của vòng tròn. Những đa giác này đi từ tam giác đều (3 cạnh, góc ở tâm 360/3 = 120 độ) đến đa giác có 360 cạnh, có góc ở tâm là 1 độ. Đặt số cạnh vào giữa dấu ngoặc đơn, ta cũng có thứ tự là tam giác đều (3), hình vuông (4), ngũ giác đều (5), lục giác đều (6), bát giác đều (8) và sau đó là các đa giác đều 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180 và 360 cạnh. Để mỗi chữ cái trong tiếng Do Thái được gán một trong những số này, theo thứ tự từ 3 đến 360.”

Tôi đã hoàn toàn bị thổi bay khi lần đầu tiên đọc nó. Đây không chỉ là một cách cực kỳ khéo léo để giải mã bảng chữ cái tiếng Do Thái với sự trợ giúp của hình học (thật trùng hợp, nguồn gốc có thể có của từ Gemaria), nó còn cho thấy một cách khá thông minh để quy các giá trị thay thế cho các chữ cái tiếng Do Thái dựa trên các đa giác mà có thể được ghi trên một vòng tròn với 360 độ. Dựa trên khám phá tuyệt vời này, Raymond Abellio sẽ tuyên bố thêm rằng sẽ có hai hệ thống Gematria chính cho bảng chữ cái tiếng Do Thái – một trong số đó là phổ biến , nghĩa là không bí mật hoặc được tiết lộ công khai

… và cái còn lại là bí mật , tức là bí mật, không được tiết lộ cho công chúng:

Một thư từ thú vị mà tôi đã tìm thấy khi nghiên cứu tác phẩm của R. Abellio liên quan đến giá trị của hai cách diễn đạt tiếng Do Thái: השמים (“ha-shamaïm”, có nghĩa là “Bầu trời”) và הארץ (“ha-aretz”, có nghĩa là “Trái đất”):

Hai giá trị này tương ứng với 38 ×7 và 29 ×7, và sử dụng cùng một mật mã, giá trị của “Eve” חוה là 29 :

… và giá trị của Elohim (được sử dụng như một danh hiệu của Chúa, mặc dù nó là số nhiều) là 83, ngược lại của 38.

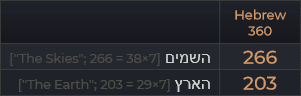
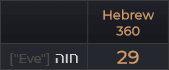
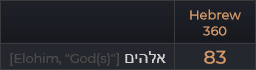
Thật không may, tôi chưa bao giờ khám phá mật mã này một cách hợp lệ trước đây, vì vậy tôi sẽ không thể hiển thị thêm bất kỳ khám phá gây tò mò nào với hệ thống này – vào lúc này. Tuy nhiên, tôi muốn giới thiệu, nếu Độc giả của tôi có thể làm được, hãy thử tìm một bản sao cuốn sách “Phép thuật: Lịch sử và các nghi thức chính” của Maurice Bouisson, hoặc có thể là một cách khác khó khăn hơn, cuốn “La Bible: Tài liệu Được Mã Hóa” của Raymond Abellio. Tuy nhiên, tôi không chắc liệu có bản dịch tiếng Anh của tác phẩm cuối cùng này hay không.

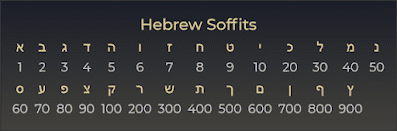
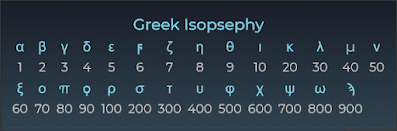
Cuối cùng, mật mã “Hebrew 360” này đã mang đến cho tôi một ý tưởng. Chẳng hạn, số 360 có chính xác 24 ước số, nhưng số 1 và 2 không được bao gồm trong mật mã “Hebrew 360” vì chúng không thể chia vòng tròn 360° thành các đa giác. Tuy nhiên, điều gì sẽ xảy ra nếu tôi sử dụng một chuỗi hoàn chỉnh gồm 24 ước số của 360 với bảng chữ cái Hy Lạp cổ điển – bảng chữ cái có chính xác 24 chữ cái?

Và từ ý tưởng này, mật mã thử nghiệm “Greek 360” đã ra đời:

Hãy nhớ rằng bảng chữ cái tiếng Anh thời Elizabeth cũng gồm 24 chữ cái, và nguyên tắc tương tự có thể được áp dụng cho nó. Tôi sẽ gọi mật mã này là “Bacon 360”, mặc dù có thể gọi chính xác hơn là “Elizabeth 360”:

Lưu ý rằng I=J và U=V, trong bảng chữ cái tiếng Anh thời Elizabeth.

Tuy nhiên, công việc của tôi với loại mật mã này chưa dừng lại ở đây. Đối với bảng chữ cái Hê-bơ-rơ và Hy Lạp, tôi cũng nghĩ rằng có thể tạo ra một mật mã khác cho các biến thể của các bảng chữ cái này: một cho bảng chữ cái Hê-bơ-rơ bao gồm các biến thể ‘soffit’ (cuối cùng) của các chữ cái Kaph, Mem, Nun, Phe và Tzaddi, và một cho bảng chữ cái Hy Lạp bao gồm các chữ cái lỗi thời Vau/Digamma, Qoppa và Sampi. Lưu ý rằng các biến thể này của các bảng chữ cái này chứa chính xác 27 giá trị khác nhau…

Vì vậy, một câu hỏi bắt đầu nảy ra trong đầu tôi: số nhỏ nhất có đúng 27 ước, bao gồm cả chính nó, là số nào? Và câu trả lời cho câu hỏi này là số 900, một trùng hợp ngẫu nhiên vô cùng thú vị, cũng là giá trị lớn nhất trong cả hai mật mã này. Do đó, dựa trên thông tin này, chúng ta có thể xây dựng hai mật mã thay thế an toàn cho bảng chữ cái tiếng Do Thái và tiếng Hy Lạp. Thay vì sử dụng cấu trúc hàng đơn vị, hàng chục và hàng trăm, chúng ta sẽ sử dụng tất cả 27 ước của số 900, từ 1 đến 900:

Với một chút sáng tạo đa dạng hơn (tôi có thể nói là một chút cầu kỳ ?), chúng ta cũng có thể áp dụng danh sách 27 ước của số 900 này cho mật mã Latinh của Agrippa, vẫn sử dụng các số từ 1 đến 900 (tuy nhiên, chúng ta sẽ chia thành các nhóm đơn vị 1-9, hàng chục 10-90 và hàng trăm 100-900 như thông thường):

Để kết luận, tôi rất cảm kích về sự chia sẻ của bạn về các mật mã thú vị này. Cách bạn đã mô tả chúng và nhấn mạnh về tính thử nghiệm và sự cẩn trọng trong việc sử dụng chúng là một ví dụ tốt về việc tiếp cận khám phá và tìm hiểu các khía cạnh mới trong lĩnh vực gematria và mã hóa. Việc chia sẻ kiến thức và ý tưởng của bạn sẽ chắc chắn đánh thức sự tò mò và sáng tạo của người đọc, và có thể mở ra những khám phá thú vị trong tương lai.

Cảm ơn bạn vì việc chia sẻ thông tin và tạo ra một không gian để người đọc khám phá và nghiên cứu thêm về các mật mã độc đáo này. Việc kết hợp sự sáng tạo với tính thực nghiệm trong việc tiếp cận gematria và mã hóa sẽ đem lại nhiều điều mới mẻ và thú vị trong lĩnh vực này.

Một số lưu ý cuối cùng

Cảm ơn bạn vô cùng vì việc chia sẻ kiến thức thú vị và sâu sắc về các loại mật mã và gematria trong loạt bài viết của bạn. Cách bạn tiếp cận việc giới thiệu, giải thích và thử nghiệm các mật mã là rất hấp dẫn và đầy cảm hứng. Các bài viết của bạn không chỉ giúp người đọc hiểu về các mật mã, mà còn mở ra cơ hội cho họ khám phá và thử nghiệm những khái niệm mới.

Tôi rất hồi hộp chờ đợi để đọc những bài viết ngắn hơn về Thực hành Gematria và những ví dụ cụ thể khác về những khám phá và ý tưởng của bạn trong tương lai. Việc bạn cung cấp cho người đọc của bạn cơ hội trò chuyện và chia sẻ ý kiến thông qua biểu mẫu “Nhận xét” hoặc “Liên hệ” cũng rất tốt để tạo ra một không gian trao đổi thông tin.

Tôi chúc bạn thành công trong những dự định tương lai và hy vọng rằng các bài viết tiếp theo của bạn sẽ tiếp tục đem lại sự thú vị và kiến thức cho độc giả của bạn. Chúc bạn may mắn và hẹn gặp lại!

Tác giả: Luís Gonçalves
Biên Dịch: Hiển Nguyễn Kabala

Gematria: “Lịch Sử Mật Mã” – Mật Mã Toán Học (V) (cập nhật 29/04/2024)

Lịch sử mật mã

của Luís Gonçalves

Kiến thức liên quan: